Introduction
Sleep sort is a very curious and original algorithm. It brings several interesting questions. Such as, how to measure its complexity or in what cases does it perform the best.
Principle
In a nutshell: for each element to sort, start a thread or a process which sleeps a time proportional to the element and then pushes it back to the main thread.
Trivial Bash implementation:
1 2 3 4 5 6 7 8 9 10 11 12 | #!/bin/bash function f { sleep $1 echo $1 } while [ -n "$1" ] ; do f $1 & shift done wait |
Test suite
In order to study it and measure its performance we (me and Hartok) decided to implement the Sleep Sort in Python and gevent.
Our program generates a set of random numbers and sorts it with Sleep sort then with the Python built-in Quick sort and records timings. It works with three parameters:
- set size
- maximum value in the set
- the ratio between sleep time and values in the set (for example with 10 the thread for 42 sleeps for 42/10 seconds)
This last parameter is pretty tricky: the higher it is, the faster the Sleep sort works. But if it is too high, the time to start a new thread (or greenlet) will be more important than the sleep time for low values and the result will be incorrect. It seems to be strongly hardware dependent and a little tied to the other parameters.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 | #!/usr/bin/python import sys import random import time import copy import gevent divisor = 900000 def sort(numbers): """ Sorts a list with Sleep Sort algorithm and measures time """ begin = time.time() def f(n, result): gevent.sleep(float(n)/divisor) result.append(n) result = [] greenlets = [] # spawn a sleep greenlet for each value for n in numbers: greenlets.append(gevent.Greenlet.spawn(f, n, result)) # wait for all greenlets to end gevent.joinall(greenlets) return (time.time()-begin, result) def systemsort(numbers): """ Sorts a list with system sort function and measures time """ begin = time.time() result = copy.copy(numbers) result.sort() return (time.time()-begin, result) def generate(n, m): """ Generates a list of n random numbers, each being less than m """ numbers = [] for i in range(n): numbers.append(random.randint(1, m)) return numbers if __name__ == '__main__': # read params try: n = int(sys.argv[1]) m = int(sys.argv[2]) except BaseException: print "usage: %s n m [d]" % sys.argv[0] print " - n number of random numbers" print " - m maximum random value" print " - d time divisor (optionnal), default is %d" % divisor sys.exit(1) try: divisor = int(sys.argv[3]) except: pass # generate random values numbers = generate(n, m) # sleep sort them (sleep_time, sleep_result) = sort(numbers) # system sort them (system_time, system_result) = systemsort(numbers) if system_result == sleep_result: print "sleep sort succeed" print "sleep: %f" % sleep_time print "system: %f" % system_time else: print "sleep sort failed (time divisor too ambitious ?)" print "sleep: (%d elements)" % len(sleep_result) #print sleep_result.__str__() print "system: (%d elements)" % len(system_result) #print system_result.__str__() errors = 0 for n in range(n): if system_result[n] != sleep_result[n]: errors = errors + 1 print "%d errors" % errors |
Test results
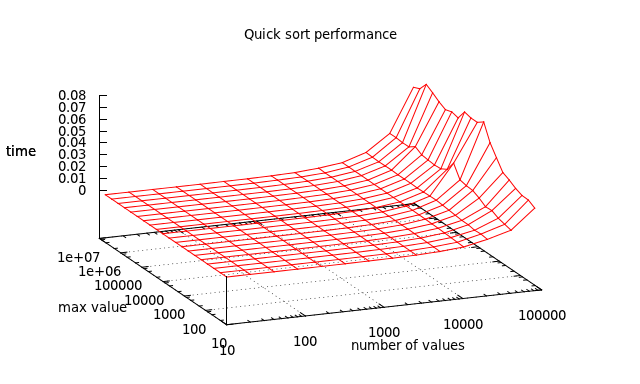
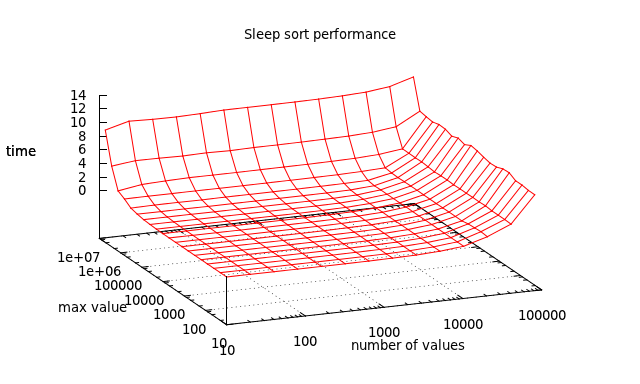
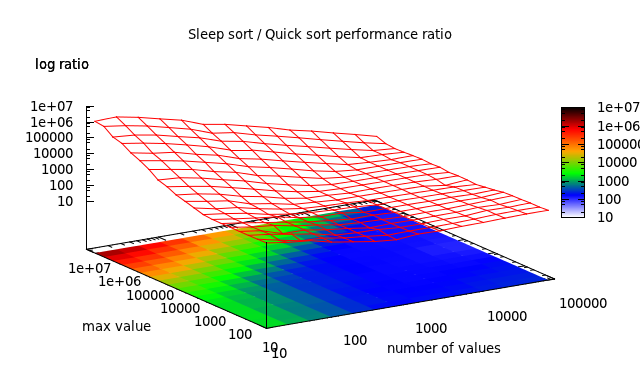
The overall performance of the Sleep sort is awful, but it has interesting performance when it comes to sets with few different values.